Ma quête vers la compression

[2022-09-29] #FSE #Algorithmie #Vie #Compression

Preface - Life post

Si vous désirez sauter cette introduction où je raconte ma vie, ce que je comprends très bien, rendez-vous directement à la section Les algorithmes de compression - début du technique !

Je me souviens avoir passé un entretien, un jour, ou j’ai dit que j’aimais bien l’algorithmie. Tout s’est bien passé, mais à la fin de l’entrevue on m’a répondu:

“C’est bizarre, tu dis que tu aimes l’algo, mais tu fais ça de cette manière ? Tout le monde sait que ça peut être résolu en O de N sur deux !”

J’avais codé cette partie sans trop me questionner. Après tout, j’allais vite, je n’ai pas pensé que justement, j’allais devoir optimiser ce bout là. Ça veut dire que je n’aime pas l’algo ? Ou bien tout simplement que je suis éclaté ? Je me posais ces questions, en plus dans une période de ma vie où je doutais un peu de ma carrière. C’était carrément un coup au moral.

Comme tout informaticien ayant fait des études de programmation, j’ai implémenté les classiques: des tris, des plus courts chemins, un allocateur, un alpha-beta pruning… et j’en passe.

Mais même en connaissant mes classiques, je pourrais mettre un peu plus de cinq minutes pour ressortir un A* parfait, sans ressource. Je ne m’exerce pas tous les jours, et le monde de l’informatique est trop grand pour tout connaître, non ? Avec du recul, je sais aujourd’hui que cette partie en entretien n’a pas été décisive. J’étais suffisamment junior pour que ça se voit, même en baratinant.

Un bon ami me dit souvent, “D’abord, implémente naïvement, ensuite réfléchis”. Et je trouve ça plutôt juste. Lorsqu’on zone là où ça parle d’algo, on tombe souvent sur quelque chose sans le vouloir. Si on est curieux, on apprend, on se rend compte de nos erreurs, on s’améliore et nos codes deviennent meilleurs. Mais le plus important est de s’amuser et de construire quelque chose.

Introduction

18 Janvier 2022. Je découvrais la série “Silicon Valley”, que je vous conseille d’ailleurs. Sans vous en dire plus, je suis instantanément allé regarder ce qui se faisait en matière de compression de données.

J’ai découvert un univers, là où moi j’en étais resté au LZW. Ce qui est genial, c’est qu’il n’y a PAS de bonne solution. Chacun a son rôle à jouer. Et si certaines méthodes ont des performances nettement plus sympas, ça ne signifie pas qu’elles sont les plus adaptées pour toutes problématiques.

Ce n’est pas tout ! Les perforances dépendent aussi des capacités hardwares ! L’amélioration de nos CPUs nous permet d’exécuter des multiplications de plus en plus vite. Les solutions de chiffrement arithmétique ont de plus en plus leur mot à dire.

“Finite State Entropy”, basé sur les recherches de Jarek Duda il y a quelques années, a vraiment titillé ma curiosité. Je n’étais pas au bout de mes peines. Car, si trouver des infos sur des algos comme celui de Huffman, ou encore Lempel-Ziv-Welch, est simple; trouver une explication abordable de FSE est très très complexe. Réservé à l’élite des gens qui écoutaient vraiment en cours de master d’info.

Zstd - L’enrôlement

J’ai commencé par passer beaucoup de temps sur le répo de zstd de Facebook. Il se trouve que FSE est libre de droits, et que zstd est open source. Et il possède parmi d’autres une implementation à laquelle Yann Collet a participé.

Comprendre par le code a souvent fonctionné chez moi. Et même si ça faisait quelques années où je n’avais pas fait du C. J’en ai quand même tiré certains éléments importants qui seront utilisés plus tard.

À propos du C:

Étudier l’informatique grâce à ce langage est exceptionnel. Mais le C a ses défauts, et le manque de lisibilité en est un. Le code du FSE est super, il est optimal pour beaucoup de points de vu. La norme actuelle est plutôt d’utiliser de la monomorphisation dans une bibliothèque, ce que le C ne permet pas facilement. En bref, une implémentation dans un autre langage ne pourrait qu’amener du positif.

Outre le langage, sans connaître les enjeux de FSE, on fait une drôle de tête devant des fonctions comme celle de normalisation. Pleines de choix techniques et d’optimisations à partir de preuves mathématiques. Sans doute pour des performances exceptionnelles, mais trop difficile à prendre en main.

Finalement, si je voulais comprendre FSE, ce n’était une bonne idée. Mais j’ai appris des choses, sur du langage C et de la culture G d’informaticien. C’est un travail qui peut être décourageant, sembler ne servir à rien, mais qui n’ait jamais une perte de temps.

Les algorithmes de compression - début du technique

Il y a deux grandes familles d’algorithmes de compression. On les connaît bien, ce sont les “sans perte” et “avec perte”. Ici, on s’interesse aux “sans perte”, pour vous citer quelques noms: LZ4, LZW, FSE, ZIP, etc.

Une bonne partie des algos utilisent des tables de compression, et d’autres non. Pour moi, les deux grandes familles sont: TABLE ou ARITHMETIQUE.

Chapitre 1, les tables de compressions - ouverture d’une parenthèse

Utiliser une “table de compression” signifie que pour un symbole, on associe une valeur.

Il y a plusieurs façons de construire ce genre de table.

En résumé, un symbole de taille 16, qui sort le plus souvent, sera remplacé par un autre symbole de taille 1. Le reste sera substitué par des symboles plus gros. L’objectif est que, même avec une répartition équitable des symboles, on gagne déjà de la place. Ça dépendra de la taille de l’alphabet aussi bien sûr.

En résumé, on associe des symboles qui, seront des lettres, à des séquences de 0 et de 1 qui seront des bits. Généralement, une lettre tient sur 8 bits avant la compression.

Si dans notre table on décide que A sera remplacé par ‘0001’, et B par ‘1’. Si B est moins fréquent que A, on n’aura pas une superbe compression. La répartition des symboles est très importante pour une bonne performance.

L’utilisation de la même méthode de compression, avec des alphabets constitués de différents symboles, aura un résultat différent tandis que la source restera identique. Par exemple pour “ABAAACABAA”, une construction d’alphabet pourrait être “A”, “B”, “C”. Ou alors “AB”, “AA”, “AC”. Le choix impactera les performances.

Zip, par exemple utilise une méthode du type Encodage de Huffman, avec une table de compression. Compresser 2 fichiers zip, peut à nouveau avoir une plus petite taille. Car les alphabets peuvent être différents. On peut aussi obtenir des résultats différents en compressant le contenu de 2 fichiers zip simultanément, ou en compressant les zips eux-même.

Ces tables sont très pratiques pour la décompression. Pas d’opérations gourmandes en CPU, on remplace des bits par un symbole. Recherche rapide, écriture rapide. Par contre la construction de la table est assez lente.

Avec une table, on peut facilement encoder et décoder “simultanément” dans le style fifo. C’est super pour de la communication réseau. Suffisamment efficace pour des petits alphabets. En plus les algorithmes sont sur Wikipédia. Comme je vous le disais, trouver des informations sur ces différentes méthodes: c’est facile !

Chapitre 2, les compressions arithmétiques, je donne un exemple

Si la l’utilisation d’une table ressemblait à $symbole \implies bits$, le codage arithmétique ressemble plus à $(état, symbole) \implies état$. En bref, on construit une machine à état.

Prenons une séquence de charactères. ABADABAC.

Dans notre exemple, on a 4xA, 2xB, 1xC, 1xD, 8 caractères au total. Donc les probabilites $P(A) = \frac{1}{2}$, $P(B) = \frac{1}{4}$, $P(C) = P(D) = \frac{1}{8}$.

Prenons un segment de taille 1. On place $a$ d’un coté et $b$ de l’autre, tel que $a = 0$ et $b = 1$. On y ajoute des repères correspondant aux probabilités des symboles. On attribut un symbole a tout ce qui se trouve entre ces repères. Le segment à gauche du repère A représente le symbole A, le à gauche du repère B et à droite A représente le symbole B, etc.

Voila a quoi ca ressemble:

Maintenant, cherchons à encoder le premier symbole de la séquence “ABADABAC”. Pour notre algorithme de compression, on doit remettre à l’échelle les valeurs de a et de b.

a devient la valeur basse de $P(A)$, et b la valeur haute de $P(A)$. Puis, entre a et b, on redispose les repères. Avant, on était à une echelle 1 $(b - a = 1)$, maintenant on est à une échelle de 0,5. Alors notre segment ressemble à ça:

Voilà, on répéte la même chose jusqu’à la fin. Pour le faire efficacement, on a besoin de deux choses:

1. Une fonction cumulative, permet de savoir où le sous-segment d’un symbole commence.

   On veut diviser le segment. Avec $P(A, B, C, D) = (0.5, 0.25, 0.125, 0.125)$. Calculer la CDF nous donne $c(A, B, C, D) = (0, 0.5, 0.75, 0.875)$, les valeurs basses des sous-segments.

2. Un cumul de la distribution ou la fréquence et de la fonction cumulative pour savoir où le symbole finit.

   $d(A, B, C, D) = (c(A) + P(A), …, c(D) + P(D)) = (0.5, 0.75, 0.875, 1)$ ce qui nous donne les valeurs hautes des sous-segments.

Remettre à l’échelle veux dire $a := a + (b - a) * c(x)$, $x$ est le caractère courrant à encoder $\in {A, B, C, D}$. Notez qu’on utilise $c(x)$ car on cherche la valeur basse. Et suivant le même principe, devient $b := a + (b - a) * d(x)$`.

a = 0, b = 1
pour chaque c dans "ABADABAC"
    w = b - a
    b = a + w * d[c]
    a = a + w * c[c]

Je bricole un petit bout de code à partir de ça et je trouve l’intervalle $[a, b)$ sans me casser la tête: $[0.3070068359375, 0.30706787109375)$. Et voilà, cet intervalle c’est notre état final. À lui seul il représente toute notre séquence encodé.

Ce qu’il faut à cette étape, c’est imaginer qu’on zoom vers la section qui représente notre symbole. Puis on remet sur cette nouvelle échelle des sections pour tous nos symboles. Un zoom égal un état, et l’état final sont les derniers $a$ et $b$.

Maintenant qu’on a l’intervalle, on peut produire une séquence binaire correspondante. Comment qu’on peut faire pour représenter un chiffre à virgule en dessous de 0 ?

En fait c’est assez simple. Si dans le monde décimal $0.1 = \frac{1}{10}$ et $0.11 = \frac{1}{10^1} + \frac{1}{10^2}$. En binaire ca pourrait etre $.1_{b} = \frac{1}{2}$ , $.11_{b} = \frac{1}{2^1} + \frac{1}{2^2}$

…ou encore $.101_{b} = \frac{1}{2} + \frac{0}{2^2} + \frac{1}{2^3}$

-- Phase 1
tant que a > 1/2 ou b < 1/2
    si b < 1/2
        produire 0
        a := 2a
        b := 2b
    sinon si a > 1/2
        produire 1
        a := 2(a - 1/2)
        b := 2(b - 1/2)

-- Phase 2
s = 0
tant que a > 1/4 et b < 3/4
    s := s + 1
    a := 2(a - 1/4)
    b := 2(b - 1/4)
s := s + 1

-- Phase 3
si a <= 1/4
    produire 0
    produire s fois 1
sinon
    produire 1
    produire s fois 0

Pas de panique, je vous explique ce qui se passe. Souvenez-vous de ce segment, on avait avec $a$ et $b$. Découpons ce segment en 2, à gauche on dit que c’est 0, à droite 1. On choisit la partie où se trouve notre intervalle. Entre 0 et 0.5, donc sur la partie de 0. Puis on double a et b. Eh oui on double ! Car l’intervalle diminue de moitié et l’échelle grandie !

On reproduit cette étape, plusieurs fois, jusqu’à ce que l’intervalle chevauche la partie gauche ET la partie droite. C’était la phase 1. À ce stade, il ne faut pas diviser le segment par deux, mais par quatre. Un schéma vaut mieux qu’un millier d’explications.

Puis observez attentivement. Vous remarquez que a commence par chevaucher ‘01’, puis ‘011’. Ce n’est pas pour rien. La tendance de l’intervalle penche plus vers la gauche, et donc naturellement, plus l’echelle grandie, plus a se rapproche de la limite gauche. Plus rapidement que b vers 1.

Un autre intervalle aura prefere tendre vers la partie droite. Les bits produit par cette phase ressemblent soit a ‘01111…’ soit a ‘1000…’ Et que le nombre de 0 ou de 1 correspond quasiment au nombre d’iterations dans la phase 2.

En résumé, la phase 3 construit les chaines, 0111… ou 1000… en fonction de si on tendait vers $a == 0$, ou $b == 1$.

Bon, il se trouve qu’avec notre répartition étrange on finit toujours avec $a = 0.5$ et $b = 0.75$ a la fin de notre première etape, et donc on produit ‘10’ en fin d’algo.

Et j’obtiens la séquence $01001110100110_b=0.3070068359375$ appartenant à l’intervalle qu’on avait trouvé.

Décoder un encodage arithmétique

Pour décoder, on reprend le premier pseudocode et on rajoute un test pour savoir quel symbole émettre.

let mut a = 0f64;
let mut b = 1f64;

// J'ai explique un peu plus haut comment faire, je reviendrais en
// detail dessus dans un autre post.
let z = bin_to_float(out);
loop {
    for n in 0..p.len() {
        let w = b - a;
        let b0 = a + w * d[n];
        let a0 = a + w * c[n];
        if a0 <= z && z < b0 {
            print!("{}", index_symbol[n]);
            a = a0;
            b = b0;
            // personellement j'ai mis C comme EOF
            if index_symbol[n] == 'C' {
                return;
            }
        }
    }
}

Fin de la parenthèse

On peut dire de nombreuses choses en plus sur ce système d’encodage. Déjà, comment gère-t-on l’imprécision du CPU ? On ne peut pas avoir une précision infinie, et une séquence du taille raisonnable dépasserait les limite imposée par la technologie. Ce n’est pas tellement une mauvaise idée d’encoder une source morceau par morceau a priori, mais ça demande réflexion.

“Même dans un Âge mythique, il doit y avoir des énigmes, comme il y en a toujours”

- Tolkien

Avez-vous essayé de compresser cette séquence, avec l’algorithme de Huffman ? Vous ne remarquez pas quelque chose ? Qu’est-ce que vous en déduisiez ?

J’aimerais vraiment en apprendre plus sur le sujet. Notamment autour des comparaisons avec Huffman ! Ainsi qu’implémenter de nouveau LZW, Huffman et un codage arithmétique scalable. Je souhaitais mettre à jour mes connaissances en compressions, et c’est chose faite. J’espère que cette parenthèse vous aura aussi plu.

Chapitre 3 - ANS, c’est quoi c’est quoi ?

FSE est une implementation qui utilise un système numérique asynchrone ! Vous n’aviez pas encore compris ?

De la meme facon que le codage arithmetique, cette methode est plutot de type $(symbole, etat) \implies (etat)$.

Le mieux c’est de commencer par un exemple. Pour FSE, on a besoin d’un histogram des symboles dans la source qu’on cherche a compresser. Par exemple, dans ABADABACA notre histogram sera [4, 2, 1, 1] correspondant respectivement au symbols [A, B, C, D]. L’ordre n’importe pas notre logique, on aurrait tres bien pu construire notre histogram [2, 1, 4, 1] correspondant a [B, C, A, D].

Je commence par calculer la somme cumulative telle que $cdf_i = cdf_{i - 1} + hist_i$ et $cdf_0 = 0$. Je reviendrai dessus plus tard, mais le maximum de ma somme doit absoluement être une puissance de 2, heureusement dans notre cas on a rien a faire car $\sum hist_i = 2^3$.

Imaginez que vous deviez construire un tableau dans lequel vous listeriez des états qui iraient de 0 jusqu’à l’infinie. Pour chacun de ces états, vous y associez un symbole. Vous savez que A aura 2 fois plus d’états que B, qui en aura deux fois plus que C ou D.

La normalisation - étape majeure de l’ANS

Construisons le même segment que tout a l’heure. Chaque partie correspond au pourcentage de chance de tomber sur un symbole A, B, C ou d. La première étape sera de s’assurer d’une chose à propos de cette distribution: Il faut que la somme de nos fréquences tienne sur une puissance de 2, la plus basse possible de préférence.

Si je reprends la chaine ABADABAC, les fréquences étaient de 4, 2, 1 et 1. Ce qui nous donne 8 ou $2^3$. C’est un peu trop simple, le calcul est déjà fait. Imaginons qu’on ait une chaine avec des fréquences telles que $freq(A, B, C, D) = (42, 23, 10, 11)$. Pour avoir une jolie répartition, il faut appliquer une normalisation.

Personnellement, j’en ai implémenté une très simple. Cette implem est loin d’être l’Unique ! Je vous laisse la liberté d’en proposer de nouvelles. Voire, d’essayer de comprendre celle de Facebook, hein, on ne sait pas hein, elle est peut-être un peu élaborée. Si l’occasion se présente, envoyez-moi vos progrès, j’y trouverai un grand intérêt.

pub fn simple_normalization(
    histogram: &mut [usize],
    cdf: &mut [usize],
    table_log: usize
) {
    let mut previous = 0;
    let max = *cdf.last().unwrap();
    let target_range = 1 << table_log; // 2 ^ table_log
    let actual_range = max;

    cdf.iter_mut().enumerate().skip(1).for_each(|(i, c)| {
        *c = (target_range * (*c)) / actual_range;
        if *c <= previous {
            panic!("table log too low");
        }
        histogram[i - 1] = *c - previous;
        previous = *c;
    });
}

J’utilise pour la première fois le concept de table_log. Cette variable, à part le fait qu’on dise qu’on doit s’aligner sur $2^{tableLog}$, a un réel impact sur la compression. Elle joue le rôle de potentiomètre concernant la vitesse d’exécution et la qualité de compression. Une table_log élevée tendra à augmenter la précision de la normalisation. Il y aura moins de 1 dans l’histogramme. Cependant, augmenter cette variable va aussi nuire à l’algorithme. Jusqu’à finir par donner une sortie plus grande que l’entrée. Baisser cette valeur a aussi un bon impact sur la vitesse d’exécution. Ça permet d’arriver moins vite à des états élevés qui prennent plus de temps de CPU pour être traités, et d’éviter des calculs superflus, on verra ça plus tard. En revanche, utiliser une valeur trop basse peut nuire à notre normalisation en la rendant impossible à réaliser, il faut trouver le juste équilibre.

1. Je calcule la fonction cumulative de mon histogramme. Mon histogramme, c’est simplement une liste de fréquences. J’applique la CDF, tel que $cdf_i = cdf_{i - 1} + freq_i$ et $cdf_0 = 0$. En suivant mon exemple, je trouve $max = 90$. J’aimerais transposer chaque valeur depuis l’échelle $[0, 90]$, sur l’intervalle $[0, 2^3]$.

2. J’applique un mapping. Vu que l’histogramme est la dérivée de ma fonction cumulative, je peux retrouver la valeur de mon histogramme à la position $i - 1$ en soustrayant previous de c. Avec ce code je devrais pouvoir retrouver $freq_{norm}(A, B, C, D) = (4, 2, 1, 1)$ avec une table_log de 3.

Le fait de devoir s’aligner sur une puissance de 2 selon moi devrait être optionnel. Ça nous permet d’accélérer l’algorithme, oui, car les multiplications peuvent facilement être remplacées par des shifts $\times{8} \iff \ll{3}$. Par contre, c’est un overhead à la compréhension de ce que fait l’algo, donc ça nuit un peu à notre expérience.

J’ai préféré ne pas retirer le concept. Étant donné que c’est quand même une partie importante. En contre-partie, je vous aiderai au moment où je considérerai qu’un petit coup de pouce est nécessaire.

Les états de l’ANS - comment ça marche alors ?!?

Reprenons après la normalisation. On a nos fréquences, on peut construire un segment de taille $\sum_{i}{freq_i}$. Maintenant, je prosose de répéter ce segment à l’infini, comme ci-dessous, et de nous poser une petite question.

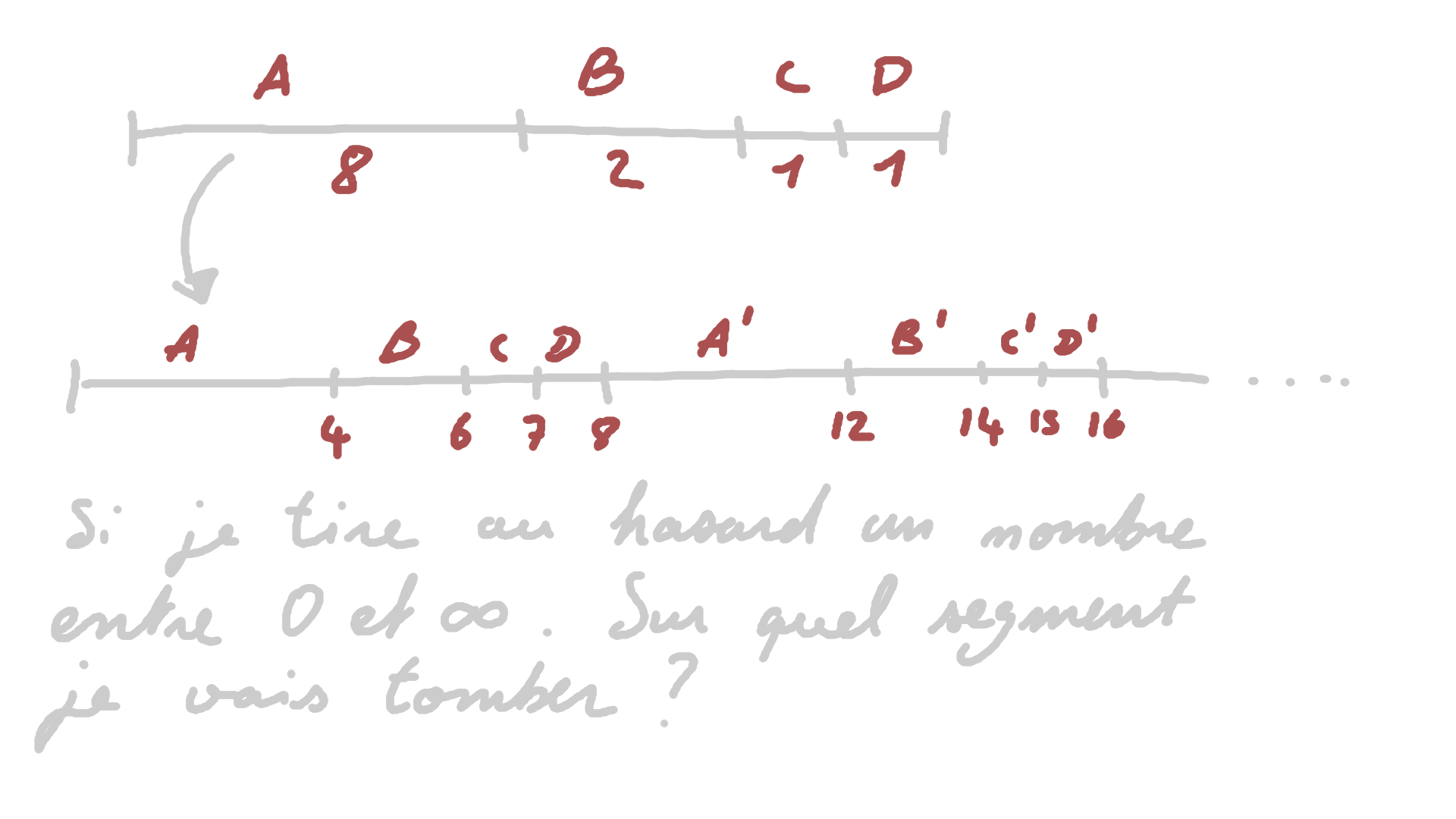
Pour commencer, je tire nombre $x$ entre 0 et 3, je tombe sur A. Entre 4 et 5, B; 6, C; 7, D. Si je tire un nombre entre 8 et 15, je devrais avoir une repartition similaire à celle entre 0 et 7. Vu que la première répartition se répète infiniement, je peux comprendre sur laquelle je suis en divisant mon nombre aléatoire par la somme des frequences $floor(x/8)$ qu’on note $\lfloor x/8 \rfloor$.

Déjà je sais si je suis sur genre X’, X’’, etc. Maintenant pour retrouver exactement sur quel symbole je suis, c’est plus compliqué. Il faut que je trouve le symbole pour lequel le cdf est le plus grand et $cdf(symbol) \leq x$. Cette recherche se fait généralement en O(n log(n)) cependant, avec un alphabet d’une taille raisonnable, la méthode des alias est envisageable pour une recherche en O(1).

Ce nombre x c’est notre état. Le principe de l’ANS nous propose un modèle qui nous permettra de trouver à partir de x l’état précédent, et en fonction du nouveau symbole, l’état suivant. Pour bien comprendre comment ça marche, il faudrait d’abord représenter une table d’état.

Dans un tableau, notez pour chaque x de 0 à l’infini, un symbole et son index. Vous pensez bien qu’on ne va pas réellement allouer une infinité d’états. Ce ne serait pas top en compression et je suis sûr que ce n’est pas tout à fait possible non plus avec nos techniques. Mais imaginez quand même:

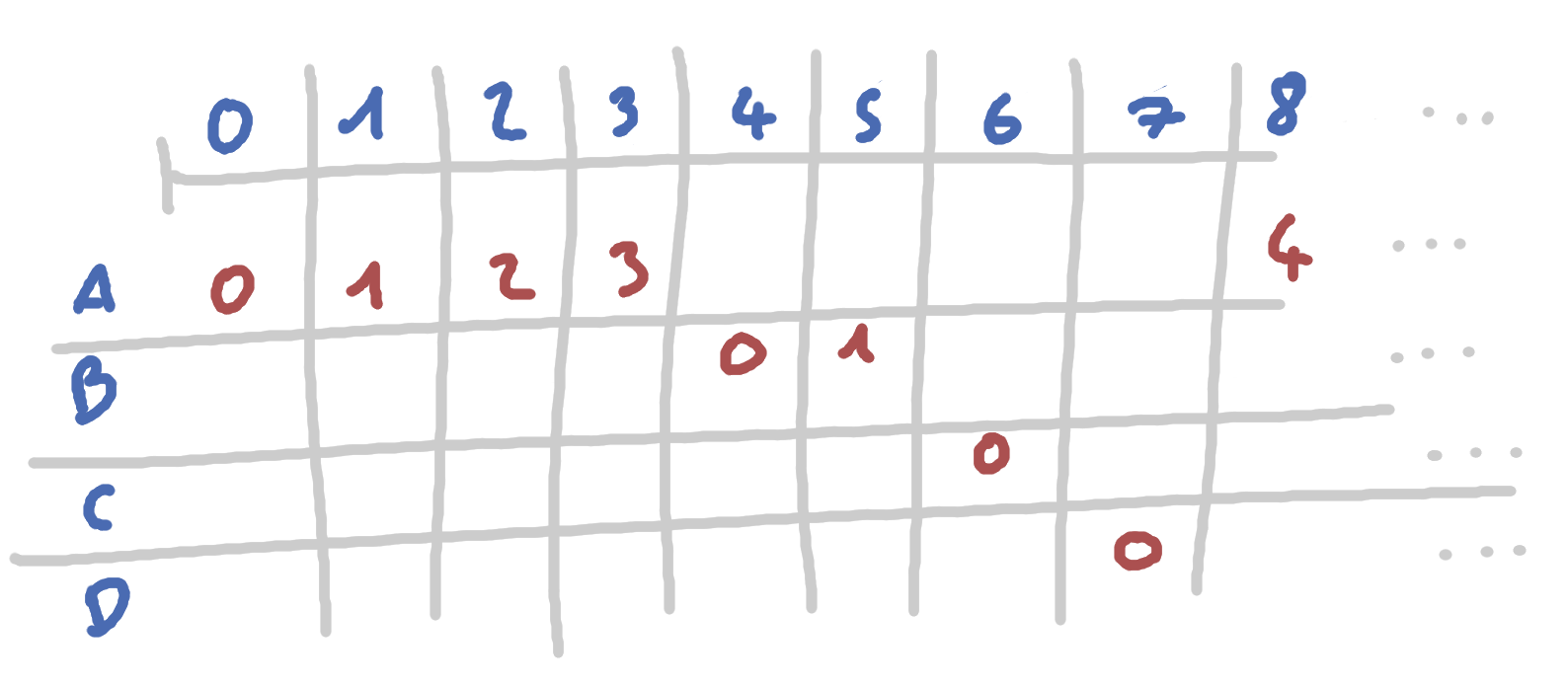
Encoder avec ANS - version facile

Disons que je suis à l’état 1, mon symbole actuel c’est A. Je cherche à encoder le symbole B, je dois trouver le prochain état correspondant. Je récupère la fréquence de B, que je divise par mon état actuel pour trouver le segment sur lequel je vais aller. Eh oui, car par segment, d’après ma répartition, j’ai $freq(B)$ symbole B.

Pour l’instant, je connais le segment, je connais aussi la taille du segment, 8. Je peux savoir grâce à ces deux informations que mon prochain état sera entre $n \times 8$ et $n\times(8+1)$. Maintenant quelle valeur exactement ça sera ?

Avec $cdf(B)$ je sais que mon premier symbole B sera à $n\times{8} + 4$. Mais je dois connaitre lequel des 2 B correspond à A en tant qu’état précédent ! C’est ça la magie ! Ma première division $n=\lfloor état/freq(B) \rfloor$ me donne le segment suivant sur lequel je peux trouver un B correspondant à plusieurs états, dont mon état actuel ! Pour le retrouver, il suffit d’ajouter l’état modulo la fréquence.

Pas facile à suivre, voici l’équation finale:

$NouvelEtat(Symbol, Etat)=\lfloor \frac{Etat}{freq(Symbol)} \rfloor \times totalFreqs + cdf(Symbol) + Etat \% freq(Symbol)$

Ici le fait d’être aligné sur une puissance de 2 nous permet de remplacer $\times{totalFreqs}$ par un shift. Le total est égal à $2^{tableLog}$ d’où $n \times{totalFreqs} \iff n \ll{tableLog}$

pub fn not_scalable_encode(
    frequencies: &mut [usize],
    // symbol_index me permet de retrouver l'index où je stocke
    // la fréquence et la cdf pour un symbole. Utiliser des
    // vecteurs, c'est pratique mais ça a aussi cet inconvénient.
    symbol_index: &HashMap<u16, usize>,
    table_log: usize,
    src: &[u16],
) -> usize {
    let mut cs = build_cumulative_symbol_frequency(frequencies);
    simple_normalization(frequencies, &mut cs, table_log);
    // Je commence arbitrairement à 1 pour mon exemple, mais le choix
    // de l'état initial peut être important.
    let mut state = 1;
    src.iter().for_each(|symbol| {
        let index = *symbol_index.get(symbol).unwrap();
        let fs = *frequencies.get(index).unwrap();
        // (floor(state / frequency) << table_log) + (state % frequency) + cumul
        state = compress(state, table_log, fs, *cs.get(index).unwrap());
    });
    state
}

Voici un peu de code qui nous montrent qu’encoder reste vraiment très simple. Je me doute que vous comprenez pourquoi ce n’est pas possible d’utiliser sérieusement ce code en production. Mais au cas où je vous donne un indice. state ne pourrait-il pas devenir un peu grand à force ?

Decoder - encore la version facile

Je pense que maintenant il faut commencer par un exemple visuel. Imaginons qu’avec le code précédent, j’ai compréssé la séquence ABA avec mon alphabet. Mon code me donnais l’état 9.

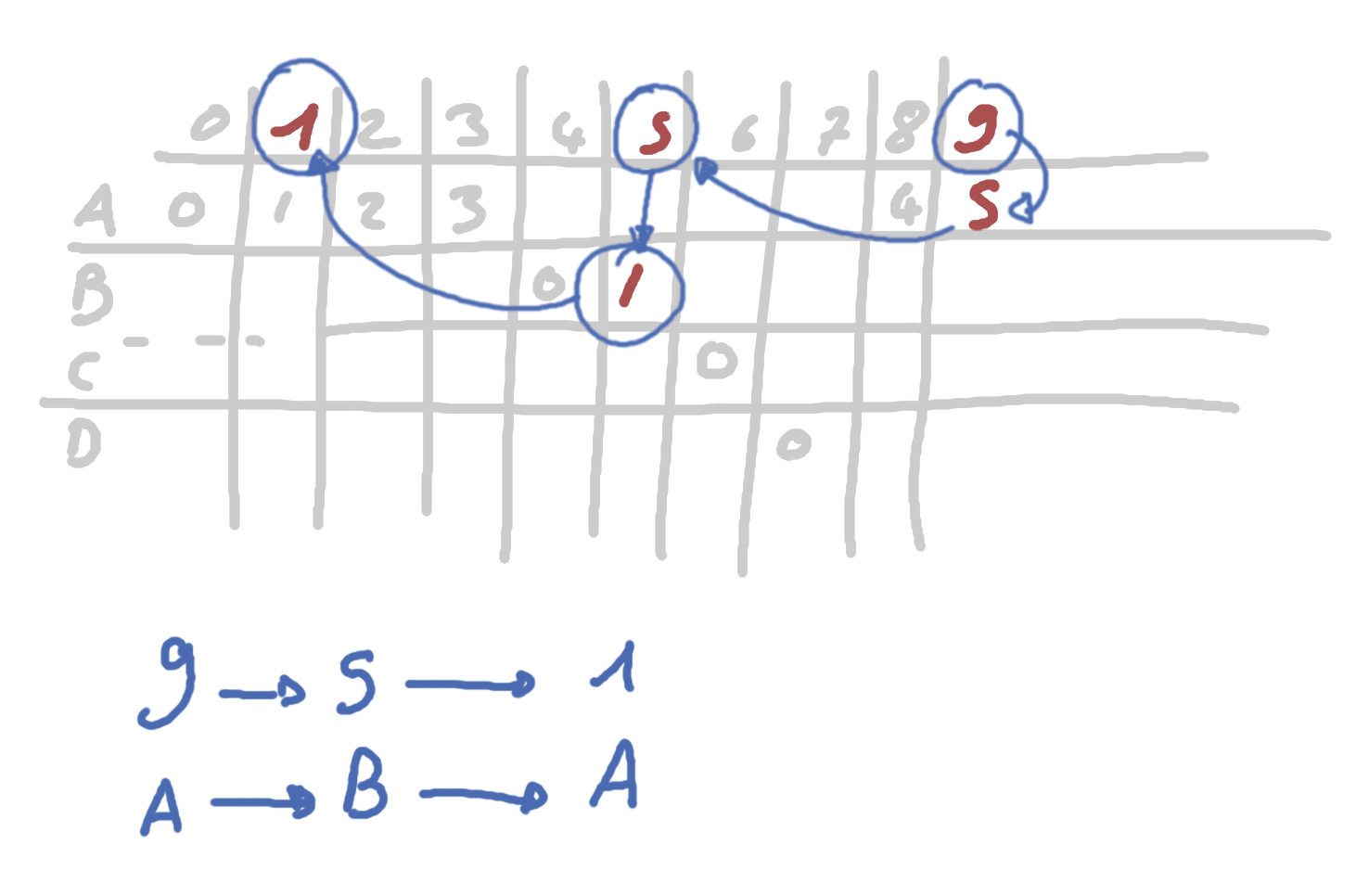
L’idée c’est que grâce à mon état, je retrouve l’état précédent avec plus ou moins les mêmes calcules que pour encoder. Je retrouve mon symbole actuel, pour pouvoir connaitre la fréquence et la somme cumulative à partir desquelles j’avais trouvé mon état à l’époque. Vous voyez la formule suivante fait exactement la même chose que pour encoder mais dans le sens inverse:

$Précédent(Etat)=freq(Symbol)\times \lfloor \frac{Etat}{totalFreqs} \rfloor + Etat \% total_freq - cdf(Symbol)$

Je vous laisse essayer, normalement vous devriez faire le même cheminement que moi. Si vous en faites un autre, demandez-vous si vous utilisez le bon symbole pour chercher la fréquence et la somme cumulative. Si vous n’y arrivez toujours pas, demandez-vous si vous savez bien calculer ?

À propos de de l’état initial

Dans mon exemple d’encodage, je vous disais que bien choisir l’état initial peut être important. Pour montrer pourquoi, mettons nous dans la situation où A est le premier symbole que je veux encoder, puis choisissons 0 comme état initial.

Pour rappel, l’équation qui me sert à trouver mon état suivant est:

$e´(s, e)=\lfloor \frac{e}{freq(s)} \rfloor \times t + cdf(s) + s \% freq(s)$

Si vous ne comprenez rien, je vous invite à remonter de deux chapitres. En attendant, voyons ce qu’$e´(A, 0)$ vaut… 0 ? Ok… $e´ = e$… Et c’est pareil pour tous mes autres symboles si je prends leurs états respectifs sur le premier segment. Eh oui.

Une tech’ pour choisir l’état initial serait de le piquer sur le second segment. De cette manière vous admettez que finir sur un état dans l’intervalle du premier segment est un signal de fin de decompression.Les mêmes solutions que celles de l’encodage arithmétique fonctionnent aussi. Par exemple, si on commence à l’état d’un EOF on va forcément avoir un état différent pour le symbole suivant. Une taille aussi devrait fonctionner.

On peut aussi faire les malins. On affirme que notre chaine commencera par A suivi d’un symbole différent. Ce n’est pas très élégant, mais efficace. À vous de voir la méthode que vous préférez. J’avoue, j’ai un peu fait ça.

Chapitre 4 - Dernière ligne droite, rendre tout ça compliqué

Vous avez dû remarquer qu’avec cette méthode, l’état final risque d’être très très grand. Il risque même très fortement d’être trop grand pour votre ordinateur. C’est pourquoi vous devriez limiter la taille de votre état à un intervalle supportable. Pourquoi pas dans l’intervalle $[2^{16}, 2^{32}]$ ? Bien sûr vous pouvez choisir cet intervalle en fonction de votre hardware.

Finalement, c’est simple. Vous prenez votre état, vous verifiez s’il n’est pas superieur à la frequence, multiplié par 2 puissance X - table_log. Dans ce cas, je shift l’état et j’écris dans un stream ce que je viens de shifter pour le relire plus tard.

let d = 32 - table_log;
let msk = (1 << 16) - 1; // 2^16 - 1

if state >= (fs << d) {
    // On recupere les 16 premiers bits
    // de l'etat actuelle et on la stoque dans un
    // stream. On shift l'etat de 16 pour guarder
    // seulement les 16 bits plus grands.
    let bits = state & msk;
    let nb_bits = u64::BITS - bits.leading_zeros();
    estream.unchecked_write(bits, nb_bits.try_into().unwrap());
    nb_bits_table.push(nb_bits);
    state >>= 16;
};

// .. encoder avec le nouvel état

On peut se demander pourquoi ce test state >= (fs << d) nous permet de s’assurer de ne pas dépasser 32 bits. Pourquoi pas simplement shifter après l’encodage ? Et bien parce qu’on est capable de savoir si on va dépasser ou non en fonction de la fréquence.

Déjà, on remarque que pour toutes fréquences dans l’histogramme, on ne dépassera jamais 2^32. C’est dû à la normalisation qu’on a appliquée précédemment. De plus, dans certains cas, encoder un symbole avec une fréquence élevée nous fera passer cette étape, alors que d’autres fréquences demanderont un shift.

$e´(s, e)=\lfloor \frac{e}{freq(s)} \rfloor \times t + cdf(s) + s \% freq(s)$

Si on prend notre exemple de fréquences avec $f_A = 4$ et $f_C = 1$, on se rend compte que $e´(A, e) \times{4} \approx e´(C, e)$ avec t une puissance de 2. De plus on se rend compte que $f_A = f_C \times{4}$. Pour être tout à fait honnête, je doute encore de mon raisonnement. Mais si mon état est inférieur à ma fréquence shiftée de 32 - table_log, il n’y a aucune raison que mon prochain état dépasse les 32 bits.

Pour décoder, c’est exactement l’inverse. J’ajoute les bits depuis mon stream, s’il y en a, pour reconstruire mon état tel qu’il devrait être.

if state < 2usize.pow(16) {
    // Si on a un état < 16, on essaye de lire le stream.
    // Dans le cas où on avait shifté, le stream contient
    // forcément des bits. Si on ne trouve pas de bits,
    // ça veut dire qu'on arrive à la fin de la decompression,
    // là où l'état a naturellement une petite taille.
    if let Some(nb_bits) = bits.pop() {
        state = (state << 16) + dstream.read(nb_bits as u8).unwrap() as usize;
    }
}

Conclusion ?

C’est un peu prématuré comme fin. Non ? Moi j’ai envie d’en savoir plus en tout cas.

Comme d’habitude, en fouillant un peu dans mon codebucket sur github vous trouverez un peu de code. Lorsque le code sera mature j’en ferai une bibliothèque bien sûr. N’hésitez pas à me poser une question sur ce répo ou en MP par mail. Je serai content de vous aider, ou du moins _essayer.

Pour l’instant, je ne peux que conclure que la compression de données, c’est compliqué. Par exemple, cet article fait une taille environ de 238000 bits. Avec un huffman et un alphabet de symboles de 8 bits, j’arrive à compresser vers 145000 bits. Tandis qu’avec FSE, sur le même alphabet, je suis à 173000.

Il y a tellement de variables à prendre en compte. Trouver la bonne répartition des symboles n’est pas évident, déjà, puis avec FSE on peut varier la précision et la taille de l’état. Ça peut tout changer ! Lorsque je compresse cet article avec un FSE et un alphabet de symboles de 16 bits, j’arrive quand même à compresser vers 138000 bits.

Enfin bref, je vous tiens au courant ! Prochaines étapes, regarder la normalisation, LZW, Huffman vs FSE et compressions arithmétiques scalables !

À bientôt !